资产管理：因子投资的系统性解析

…

CAPM

• 无风险资产的事前回报率和事后回报率是相等的
• risk premium 是风险资产 和 无风险资产的事前回报率之差

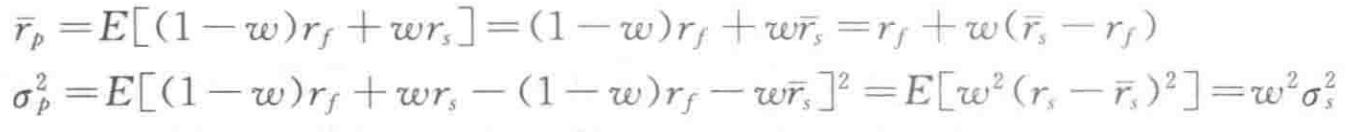
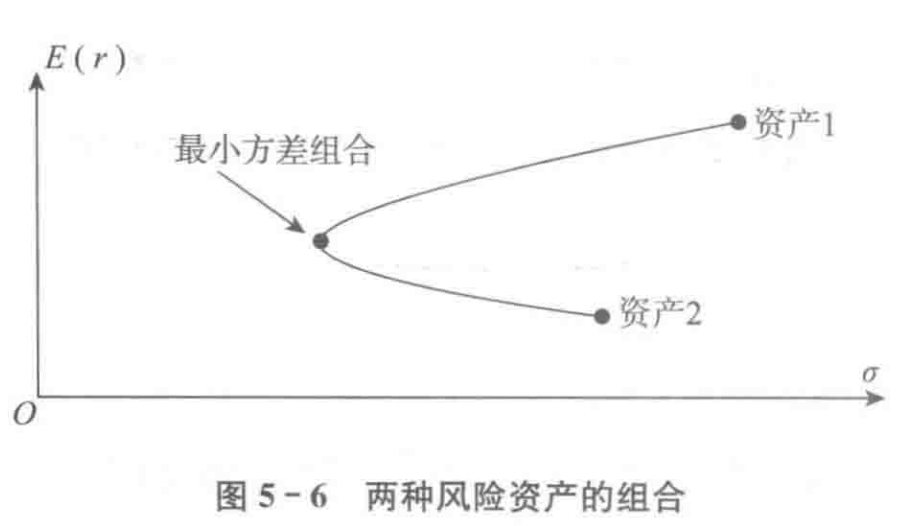
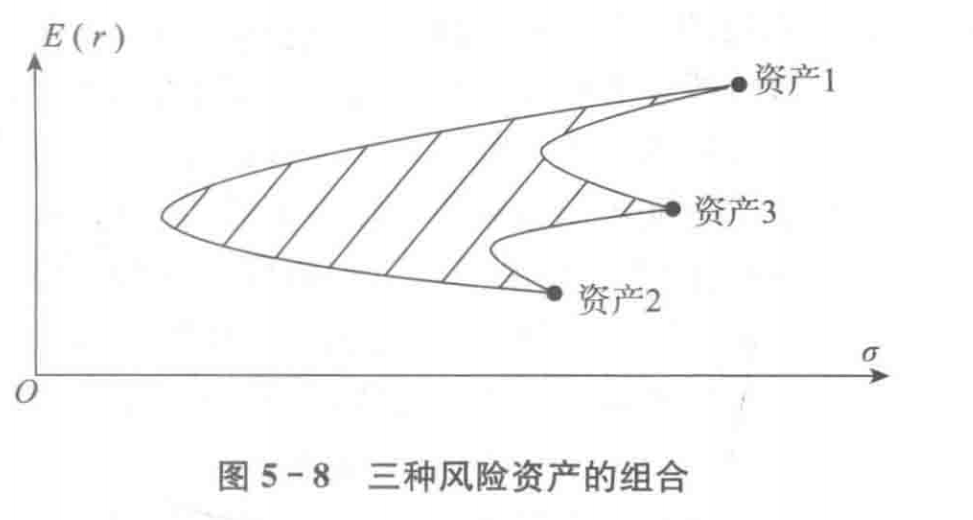
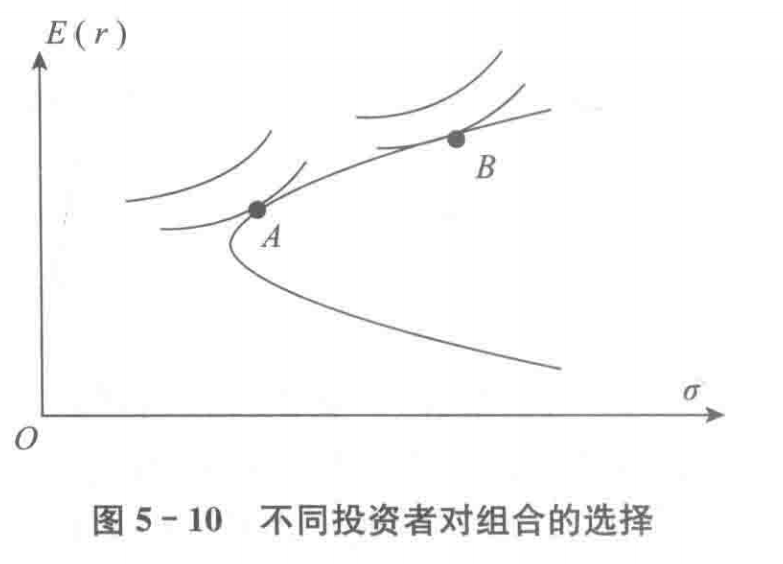
资本市场线 CML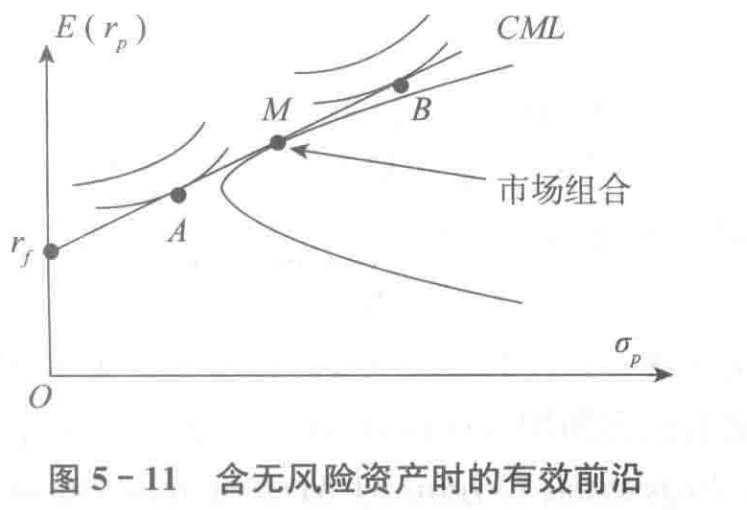

• A和B有不同的无差异曲线，但都会选择同样的风险资产组合，即市场组合，差异只是分配在无风险资产和市场组合上的财富比例不同

基于效用函数的CAPM论证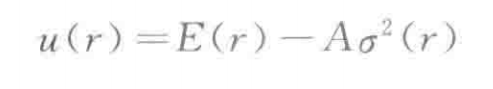

• 假设某个投资者持有市场组合M，此时分配w给新的资产i，如果M是最优选择，那么边际效用为0，算出来即CAPM
  

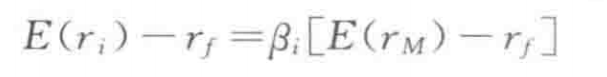
基于组合构建的CAPM的论证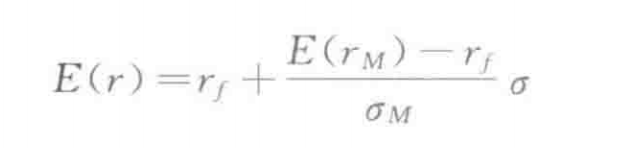

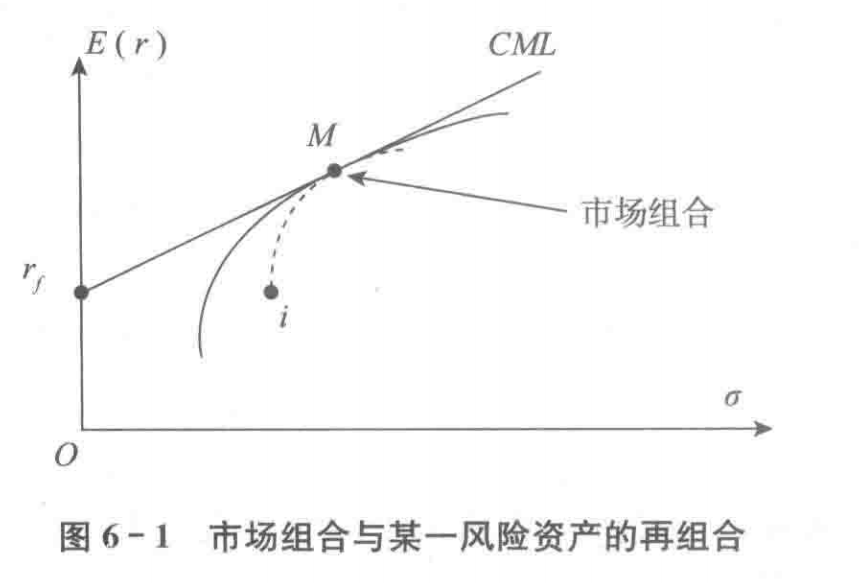
• 开始处在资本市场线上，如果组合M和新资产i，则新的组合和资本市场线相切于M，斜率相等算出CAPM

证券市场线 SML

• SML中，风险用β衡量，风险的价格是E(rm)-rf；CML中风险用σ衡量，风险的价格是(E(rm)-rf)/σm

CAPM的缺点

• 只是pertial equilibrium，将宏观环境当做外生给定
• 静态模型，只研究单期决策

资产管理：因子投资的系统性解析

一些策略

• 均值方差策略
• 市值权重
• 多样化权重：Fernholz, Garvy, Hannon(1998)，市值权重变换
• 等权重
• 风险均配：资产权重和反差倒数成比例
• 最小方差：均值方差前沿最左端
• 等风险贡献
• Kelly Rule策略
• 与夏普比率成比率策略

长期投资

• 动态再平衡策略：逆周期的，卖出上期表现好的，买入上期表现不好的
  用二叉树构建60%股票和40%固定收益的债券，比较再平衡和买入并持有，再平衡相当于卖空价外看涨或看跌期权，即卖空波动率

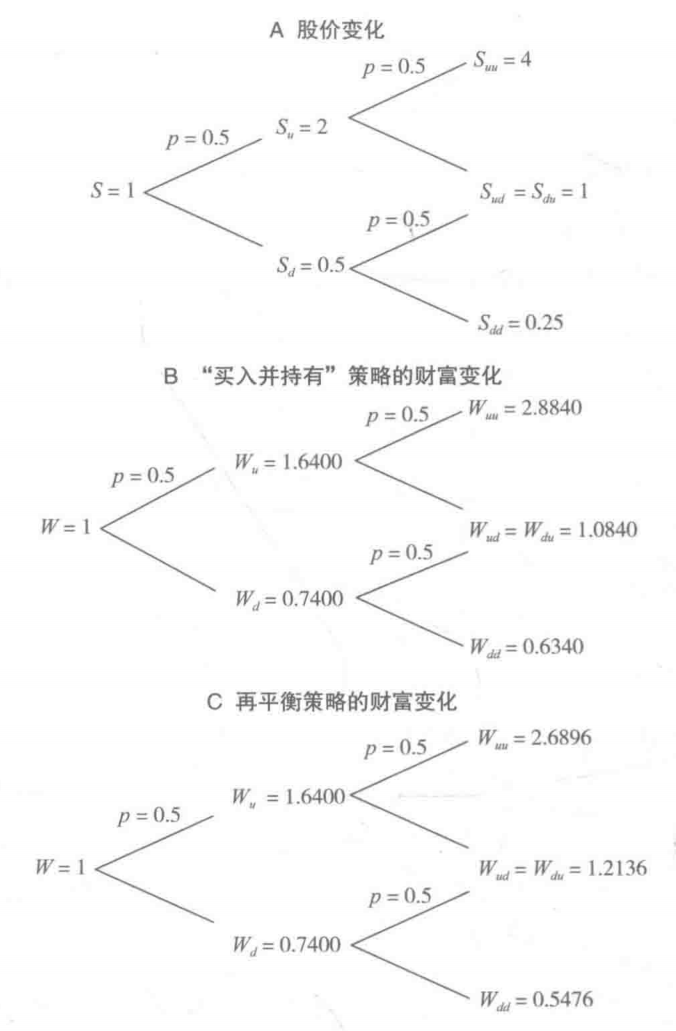
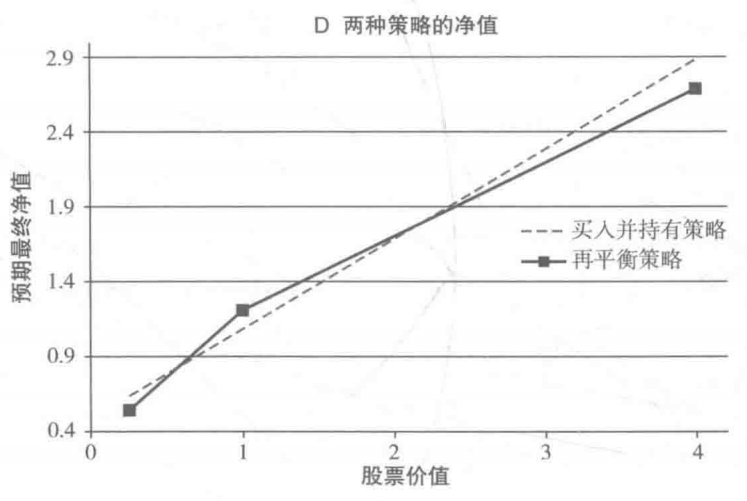
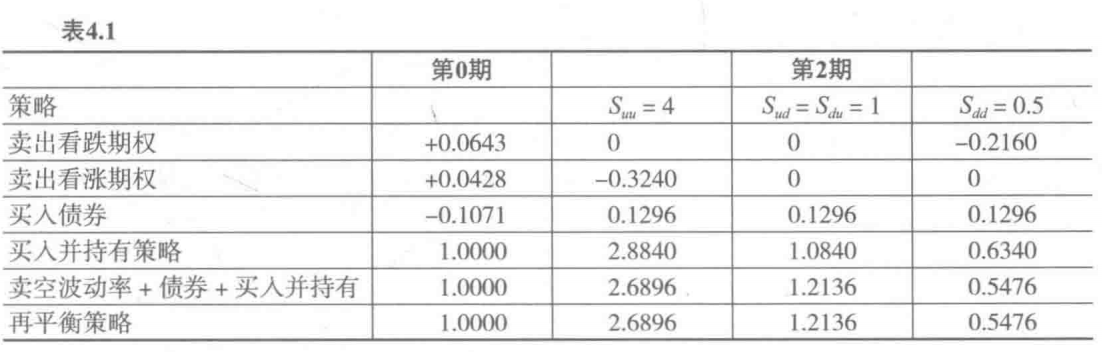
因子理论
CAPM结论

• 别持有单个资产，应持有因子
• 投资者有各自的最优因子风险敞口
• 平均投资者持有市场组合
• 因子风险溢价具有经济意义：风险计价 = 平均的风险厌恶程度 * 市场组合的波动率（对CAPM的第一种理解）
  
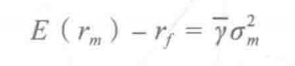
• 风险源于因子敞口（对CAPM的传统理解）

多因子模型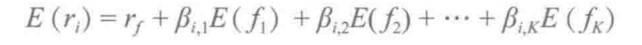

CAPM的缺陷（假设）

• 投资者只有金融财富：人力资本？
• 投资者具有均值方差效用：真实的效用函数对风险往往不对称
• 单一投资期
• 投资者具有同质化预期
• 没有税收或者交易成本
• 单个投资者都是价格接受者
• 信息是免费的，所有投资者都能获取

因子

• 宏观因子
  • 通胀
  • 经济增长
  • 波动率：通常和股票负相关
  • 生产率
  • 人口结构风险
• 动态因子
  • Fama-French
  • 规模因子
  • 价值因子
  • 动量因子：做多过去一段时间表现好的，做空表现差的
    

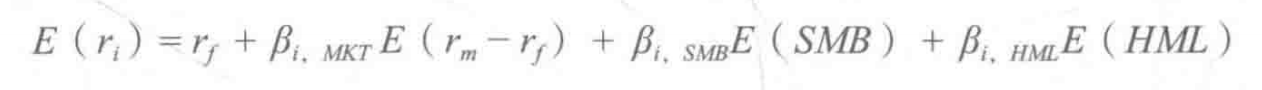
阿尔法

• α
• Tracking Error
• Information Ration = IR = α/ σ
• 当基准利率是无风险利率时，IR就是sharpe ratio

• CAPM对巴菲特持仓回归
  

• Fama-French模型对巴菲特持仓回归